Varational Fluid Mechanics
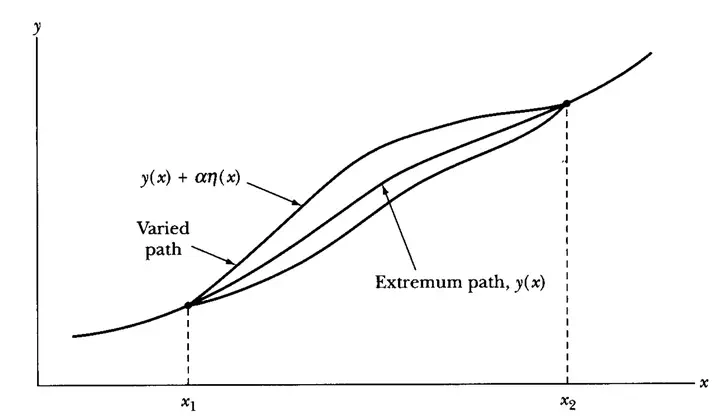 A variation.
A variation.A primary goal in the study of fluids is to describe the motion of a fluid system in response forces. There are two main paradigms in it’s parameterization, the spacial Eulerian description and the material Lagrangian description. Despite their differences, it is clear that they must agree in their predictions. This would imply there is some method of transforming back and forth between them. Despite the plausibility of such a transformation, simple ideas in one description turn out to be not so simple in the other. A primary example of this is the principle of least action and Hamilton’s equations of motion from classical physics with point particles. To extend the particle based formalism into a Lagrangian description one just needs replace the summation with an integral over the material body. However, if you apply this formalism directly to the Eulerian description the solutions are always the trivial motionless velocity field
To view this project please click on the PDF link above.